4 Applications
Sociality’s role is to study the teachers’ professional development journeys, curate and co-produce software and workflows that address gaps and bottlenecks in understanding. Over nearly 20 years of work we have created many applications - ranging from virtual rods, puzzles and games (Whiteboard, Interactive Quicktime, HTML, iOS).
Three are illustrated here: an application by Nrich of the virtual rods, notHiding by Ian Benson and a tiling puzzle by Greg Gomberg. The puzzle was developed to stimulate discussion at the ATM conference Computational Thinking in Mathematics strand at the virtual conferences in 2021 and 2022. Here you can read a report and watch the proceedings.
4.1 Virtual rod environments
Once our own HTML and teacher developed whiteboard applets were superceded we created a webpage that linked to the nrich virtual rod environment and the public domain version of gattegno (formerly Numbers in Colour).
mathigon number bars are another virtual rod resource. Unlike nrich mathigon chose to label the rods with their number names when measured with a white rod.
4.2 Gattegno code pelmanism
notHiding is an iOS (iPhone and iPad) application for toddlers, pre-school children and their parents. It helps to improve your child’s ability to take turns, learn, sort, recall, name and code Cuisenaire® colors, using capital or lower case letters.
The game can be played in one or two player mode to stimulate conversation and discussion about game strategy. The object of the game is to turnover cards to complete a pattern of matching pairs.
There is one level of difficulty on the iPhone and two on the iPad matching
- pairs of colour cards selected at random from a palette of 10 Cuisenaire® colors
- pairs of random capital letters
- pairs of minuscule letters
- pairs of matching capital and minuscule letters
- pairs of matching Gattegno colour codes and Cui colors
In single player mode the object is to uncover all the cards. This exercises memory and the ability to name the individual colours, letters and codes. Once this is mastered a more difficult challenge is to uncover all the cards with the smallest number of taps. The learner can keep count of how near they are to this target, and note how their score improves with practice.
In two player mode the object is to turn over more pairs than your partner. Players who successfully turn over a pair will take the next turn. The game keeps count of the score, and regulates turn taking.
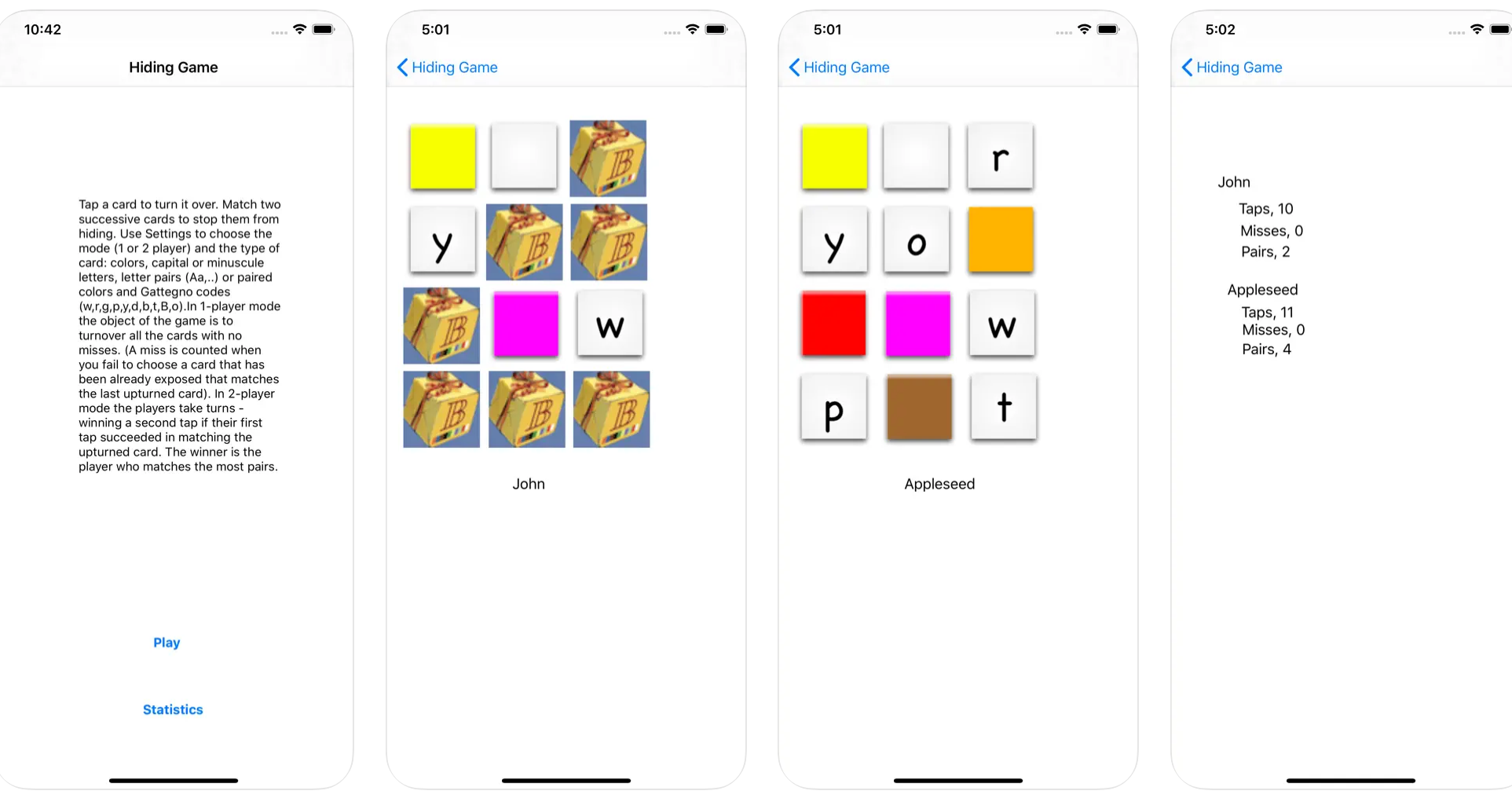
Figure 4.1: notHiding: an iOS app for parents and toddlers
4.3 Tiling Puzzle
Greg writes in this app “Computational Thinking has become a popular and apparently respectable concept, particularly in education, but I am not at all comfortable with it. It is a rebranding of a selection of mental tools (thought processes), and the danger is that enthusiasm for Computational Thinking will result in pupils being restricted in their thinking because they lack the tools that happen not to be in that selection. My personal view is that Computational Thinking is just a subset of mathematical thinking, but we do not need to argue about that. The point I want to make is that it does not cover all the tools one needs for computer coding, let alone for real life. Generations of social forces and poor education have made”Mathematics” a poisonous brand for pupils at school and for people who are highly educated in non-numerate disciplines. So I can see that inventing a new brand might seem a good idea. However, the descriptions I have found of Computational Thinking omit important parts of the mathematical thinking toolkit and that makes concentration on Computational Thinking dangerous.
“Here are some examples of an old family of puzzles you may have met before. I want to remind you of these - or introduce them if they are not familiar to you - because they provide an example where understanding requires the use of tools that are missing from the Computational Thinking kit - in this case, the concepts of symmetries and invariants - two sides of the same mathematical coin.
“If it were just a matter of puzzles then this would not be important. However, there are real-world practical problems whose abstract models are very like these puzzles, though more complicated. If, say, you accepted the task of coding an algorithm to help with one of those problems then you would probably start by making an abstract model similar to these puzzles and code your algorithm to solve that. Computational Thinking would certainly be necessary, but would not be sufficient. If you didn’t use tools that are missing from Computational Thinking then the success of your algorithm would be a matter of luck.
“A well-rounded syllabus ought also to include other, less mathematical modes of thought. We need people to grow up with a better understanding of Scientific Thinking, Logical Thinking, Statistical and Probabilistic Thinking, Ethical Thinking, Thinking about Risks, Skeptical Thinking, Historical Thinking and so on. Overselling”Computational Thinking” certainly threatens the rest of mathematical thinking, but it looks likely to threaten these other capabilities as well.”