3 Method of Approach

3.1 Co-design principles

We have pioneered a unique co-design approach to working with stakeholders - parents, pupils, teachers, academic researchers and government - on innovation in the school curriculum.

Figure 3.1 is a cartoon that illustrates our approach. It formed part of our annual report to stakeholders in 2008. The signpost points to the various Stanford and Cambridge University libraries where we conducted desk research. Teachers in Devon and Leicestershire and head teacher Steve Clarke are shown recording learners at work for subsequent analysis and INSET. The red box of Cuisenaire rods, together with our interactive Quicktime virtual manipulative ribbon, shows the objects we use to design “mathematising situations.”

In the background are sketches of Dick Tizard (1917-2005) and Kristen Nygaard (1926-2002). This acknowledges their role in pioneering outreach, conceptual modelling and participatory design. Sarah Brown, the wife of the Prime Minister (2007-10), is photographed visiting our exhibition stand at the Labour Party conference. Gordon Brown’s Policy Unit took a close interest in our work. Its head, Dan Corry, arranged for Sir Jim Rose, a member of the Williams Committee on Primary Mathematics, to visit Stockland School. Rose’s positive assessment of the Cuisenaire-Gattegno approach is reproduced in the Front Matter.

Figure 3.1: A virtual college

Our approach to the participatory design of teaching and learning resources, including software, has its foundation in Gattegno’s characterisation of the unfolding of mathematical activity. He illustrated this in Figure 3.2 (Catir and Gattegno 1973) where he describes mathematical activity as unfolding through:

• Action using the number array, the set of fingers, rods …

• Virtual action using imagery generated by the action

• Speaking language to describe the imagery

• Writing symbols and notation.

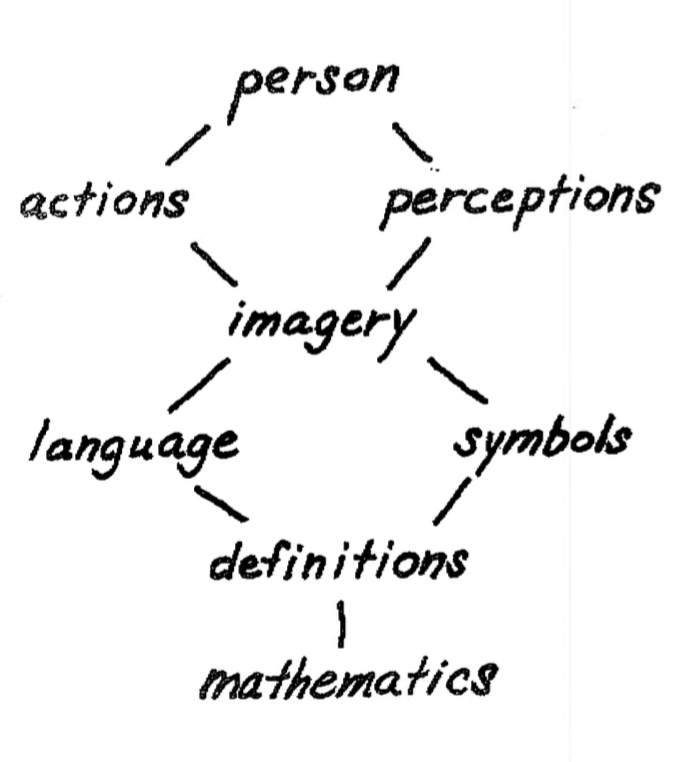
Figure 3.2: The unfolding of mathematical activity

3.1.1 Cycles of work

Our first step was to abstract Gattegno’s process and embed it into a cycle of work (CoW). This meant that teachers could use his analysis to distinguish the stages in development of the learners mathematics from their own developing “meta-mathematical” awarenesses.

Figure 3.3 illustrates the dialogue between the teacher (on the left) and the learner (on the right) as a “conversation for action.” This is a choreographed set of speech acts documented in (Winograd and Flores 1986). We use the notation of the London Underground map Figure 3.3 to highlight decisions made by the teacher and learner from labels for activity that move the process on. Unlike Gattegno we permit the possibility that the learner is operating simultaneously at both imagining and recognising a mathematical situation.

The figures below are taken from (Benson 2011) (pages 10 and 44). They were introduced at INSET sessions for the Leicestershire schools with the DfES Director of Strategy, Michael Stephenson and at a workshop with teachers at Stockland in June 2007.

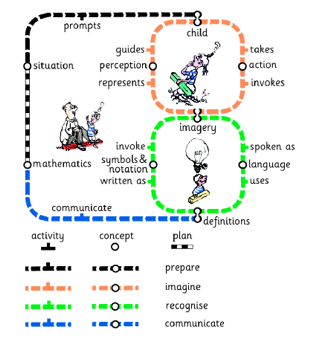
Figure 3.3: A cycle of learning and teaching

3.2 Meta-mathematics

The next step was to develop a meta-mathematical account, in conceptual mathematics, that could succinctly model what the teachers were learning about how to think algebraically about the structure of number systems (Cheng 2022)

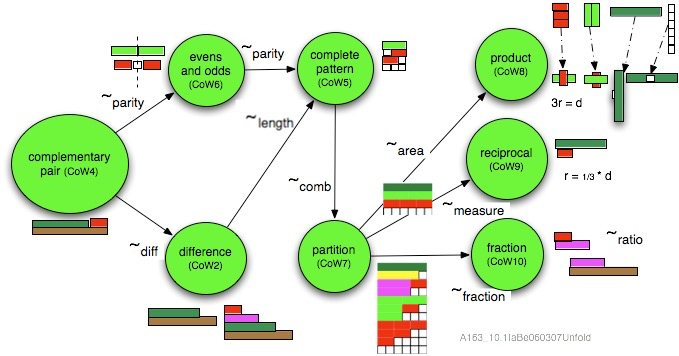
Figure 3.4: Cycles of work to cover primary maths

Ten cycles of work were abstracted from (Gattegno 1986), 8 of which are recorded in the diagram, Figure 3.4. This shows the interdependencies between cycles as domains of reasoning. Each domain is a category of rod constructions with an organising equivalence relationship: length, parity etc (Cheng 2022).

Early algebra is now seen as an important area of educational research and we were able to test our developing understanding with peer review at meetings of the ATM/MA Primary Expert group report by Fran Watson of nrich May 2016 and at several ATM conferences. Susan Empson et al are typical of this developing consensus when they write: “We suggest that a model of the development of children’s understanding of arithmetic that is based upon a concrete to abstract mapping is too simplistic. We propose instead that developing computational procedures based on relational thinking could effectively integrate children’s learning of the whole-number and fraction arithmetic in elementary mathematics, in anticipation of the formalization of this thinking in algebra.” The Algebraic Nature of Fractions: Developing Relational Thinking in Elementary School , Susan B. Empson, Linda Levi, and Thomas P. Carpenter, in Early Algebraization, eds Jinfa Cai and Eric Knuth, Springer, 2011, p 411

Jenny Cane and Ian Benson elaborated one such approach to meta-mathematics at the Primary Expert Group in May 2016. We illustrated a unified pathway from primary mathematics to informatics (computer science), the natural sciences and secondary mathematics Figure 3.5.

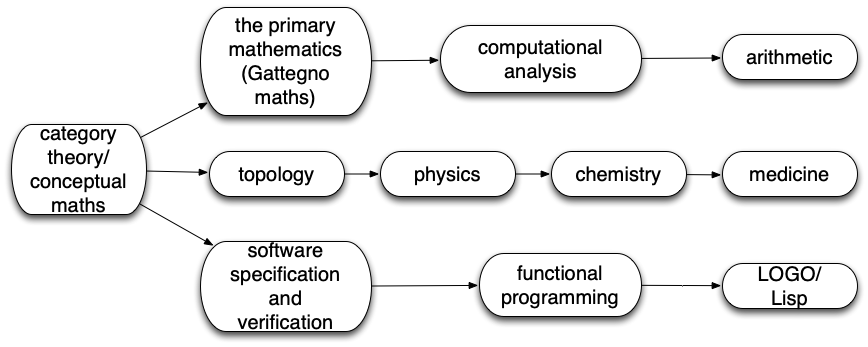
Figure 3.5: The Primary Mathematics (Curriculum Zero)